¿Qué son las fracciones equivalentes?
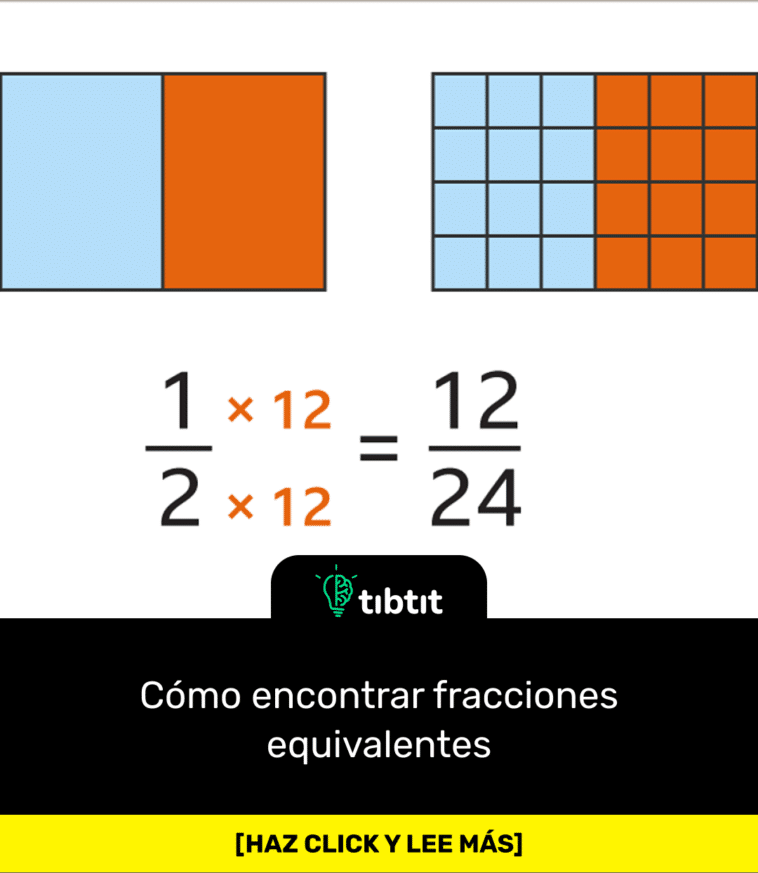
Las fracciones equivalentes son dos o más fracciones que contienen números diferentes entre sí, pero en realidad son la misma cantidad. Por ejemplo, podemos ver en la imagen de arriba que 1/2 y 2/4 son la misma cantidad aunque se escriban diferente. En esta guía veremos por qué las fracciones equivalentes son útiles y cómo encontrarlas.
¿Por qué son útiles las fracciones equivalentes?
Las fracciones equivalentes son realmente útiles en varios escenarios. Una es cuando se trata de escribir una fracción en una forma más simple, por ejemplo, ¿tiene más sentido 8/16 o 1/2? Ambos son exactamente la misma fracción, pero estamos más acostumbrados a usar 1/2 y tiene más significado en el uso diario.
Otro uso es cuando se compara el tamaño de diferentes fracciones. Puede que no sea inmediatamente obvio cuál es el mayor entre 4/5 y 17/20, pero se pueden usar fracciones equivalentes para compararlos. Veremos este ejemplo en particular más adelante.
El tercer uso que veremos aquí es cuando sumamos o restamos fracciones. Si tratamos de sumar 1/2 y 1/3 juntos, encontraremos esto extremadamente difícil sin primero usar fracciones equivalentes.
Cómo encontrar fracciones equivalentes
Comencemos con la fracción 2/3. Tener 2/3 de algo solo significa que lo dividiste en 3 partes iguales (este es el número en la parte inferior de la fracción, también conocido como el denominador) y tomaste 2 de estas partes (este es el número en el parte superior de la fracción, también conocido como el numerador).
Para encontrar una fracción equivalente a 2/3, observemos la siguiente imagen.
Convertir 2/3 en 4/6
El rectángulo de la izquierda se ha cortado en tercios y se han coloreado dos para representar 2/3. Si cortamos cada uno de estos tercios en dos partes iguales como se muestra en el rectángulo de la derecha, no solo tenemos el doble de partes en total, sino que también tenemos el doble de partes coloreadas. Esto significa que hemos duplicado tanto el denominador como el numerador para obtener 2/3 = 2×2 / 3×2 = 4/6.
Podemos ver en la imagen que la cantidad de rojo no ha cambiado; ambos son definitivamente la misma proporción del rectángulo. Podemos decir por tanto que 2/3 y 4/6 son equivalentes entre sí.
También podemos hacer esto con otros números. Echa un vistazo a la imagen de abajo.
En este ejemplo, hemos dividido el rectángulo original cinco veces más. Podemos ver que tenemos cinco veces más bloques en total y cinco veces más bloques sombreados, por lo que hemos multiplicado tanto el numerador como el denominador por 5 para obtener 2/3 = 2×5 / 3×5 = 10/15. Una vez más, podemos confirmar que esto es cierto mirando el diagrama. Ambos rectángulos muestran la misma cantidad sombreada, por lo que 2/3 es igual a 10/15. Son fracciones equivalentes.
La forma rápida de encontrar fracciones equivalentes
Los diagramas que hemos visto hasta ahora son excelentes para ilustrar cómo funcionan las fracciones equivalentes, pero no los necesitamos para los cálculos reales. Todo lo que necesitamos hacer es multiplicar tanto el numerador como el denominador por el mismo número para convertir una fracción en una equivalente.
Ejemplo 1 – Encuentra tres fracciones equivalentes a 3/4
Para cada fracción equivalente solo tenemos que elegir un número por el que multiplicar el numerador y el denominador. 2 es fácil para empezar.
3×2 / 4×2 = 6/8
Usemos 5 y 8 para encontrar dos fracciones equivalentes más.
3×5 / 4×5 = 15/20
3×8 / 4×8 = 24/32
Entonces 3/4, 6/8, 15/20 y 24/32 son todos equivalentes.
Ejemplo 2: convertir 2/5 en una fracción equivalente sobre 20
Para resolver esto necesitamos calcular qué multiplica nuestro denominador actual de 5 para dar el denominador requerido de 20.
20÷5 = 4
Como el denominador se está multiplicando por 4, debemos hacer lo mismo con el numerador.
2×4 = 8
Por lo tanto 2/5 = 8/20.
Usar la equivalencia para simplificar fracciones
Hemos visto cómo multiplicar arriba y abajo por el mismo número produce fracciones equivalentes. Al invertir el proceso, también podemos ver que dividir arriba y abajo por lo mismo también producirá fracciones equivalentes.
Si podemos dividir arriba y abajo hasta que lleguemos a un punto en el que ya no haya un factor compartido para dividir (que no sea 1), entonces hemos simplificado la fracción.
Ejemplo 3 – Simplificar 2/12
2 y 12 son múltiplos de 2, por lo que podemos dividir el numerador y el denominador por esto para simplificar la fracción.
2/12 = 2 ÷ 2 / 12 ÷ 2 = 1/6.
Ejemplo 4 – Simplificar 8/20
A veces es posible que necesitemos dividir más de una vez. Simplifiquemos 8/20. Nuevamente, ambos números son pares, así que comencemos dividiendo por 2.
8/20 = 8 ÷ 2 / 20 ÷ 2 = 4/10
4 y 10 también son pares, por lo que podemos reducir a la mitad nuevamente.
4/10 = 4 ÷ 2 / 10 ÷ 2 = 2/5.
2 y 5 no comparten ningún otro factor que no sea 1, por lo que hemos simplificado por completo.
Por lo tanto 8/20 = 2/5.
Por supuesto, si hubiéramos notado que nuestros números iniciales de 8 y 20 son ambos múltiplos de 4, entonces podríamos haber dividido por esto para obtener nuestra respuesta final de una sola vez. No importa cuántos pasos des, igual llegarás a la misma respuesta final simplificada.
Usar fracciones equivalentes para comparar fracciones
Al comienzo de esta guía, mencionamos comparar 4/5 y 17/20. ¿Cuál es más grande? Al usar fracciones equivalentes para que los denominadores sean iguales, podemos resolver esto rápidamente.
5 cabe en 20 4 veces, así que multipliquemos arriba y abajo de 4/5 por 4.
4/5 = 4×4 / 5×4 = 16/20.
Está claro que 17/20 > 16/20, por lo que 17/20 es la mayor de nuestras dos fracciones.
Usar fracciones equivalentes para sumar y restar fracciones
Solo es posible sumar o restar fracciones manualmente , cuando las convertimos en fracciones con denominadores coincidentes.
Por ejemplo, ¿cuánto es 1/4 + 3/8?
Podemos usar lo que ya hemos aprendido para convertir 1/4 en 2/8. Ahora tenemos:
1/4 + 3/8 = 2/8 + 3/8 = 5/8.
A veces, es posible que necesitemos convertir ambas fracciones para que los denominadores coincidan.
Ejemplo 5 – ¿Cuánto es 1/4 + 3/8?
Por ejemplo, ¿cuánto es 1/4 + 3/8?
Podemos usar lo que ya hemos aprendido para convertir 1/4 en 2/8. Ahora tenemos:
1/4 + 3/8 = 2/8 + 3/8 = 5/8.
Ejemplo 6 – ¿Cuánto es 3/5 + 1/6?
A veces, es posible que necesitemos convertir ambas fracciones para que los denominadores coincidan. Por lo general, la forma más rápida de hacer esto es buscar el mínimo común múltiplo de los dos denominadores.
LCM(5,6) = 30, por lo que debemos convertir ambas fracciones en trigésimos.
3/5 + 1/6 = 18/30 + 5/30 = 23/30.
Resumen de fracciones equivalentes
- Las fracciones equivalentes son fracciones que son iguales entre sí.
- Podemos encontrar fracciones equivalentes al multiplicar (o dividir) tanto el numerador como el denominador por el mismo número.
- Para comparar o sumar/restar fracciones, primero use fracciones equivalentes para asegurarse de que sus fracciones tengan el mismo denominador.