¿Qué es la derivada de una función?
En cálculo, la derivada es la herramienta que se utiliza para determinar la recta tangente a una curva que representa una función en un punto. La ecuación de la derivada, cuando se evalúa en un punto específico, da la pendiente de la curva en ese punto.
Primero, debemos aclarar el concepto de recta tangente. Una tangente a un círculo es una línea que toca el círculo en un punto. Pero, para una curva general, una línea tangente es una línea que tiene la misma pendiente que la curva en un punto. Si la tangente cruza la curva, intersecta la curva varias veces o simplemente toca la curva una vez, no es lo que determina que una línea sea tangente a una curva. Es la línea que más se aproxima a la curva en una distancia incremental.
Más formalmente, para encontrar la derivada de una función en el punto ( a , f ( a )) comenzamos con la gráfica de f ( x ). Ahora elige un segundo punto ( a + h , f ( a + h )) y conecta los dos puntos con una cuerda para la gráfica de la función. Si h es arbitrariamente pequeño, la pendiente de la cuerda es una buena aproximación a la pendiente del gráfico. Si tomamos el límite cuando h tiende a 0, llegamos a la pendiente de la recta tangente. Hay que aclarar que h puede ser positiva o negativa. Ya sea que la cuerda esté a la derecha o a la izquierda de un punto, la tangente debe ser la misma si existe.
No todas las funciones tienen una derivada en todas partes. Si el gráfico tiene un cambio brusco en la pendiente, como lo hace el gráfico de la función de valor absoluto de x en x = 0, la función de valor absoluto no tiene derivada cuando x = 0.
Otro problema ocurre cuando una función es discontinua en un valor de la variable independiente. En discontinuidades, la tangente no existe, por lo que no hay derivada.
En resumen, existe una derivada donde una función es continua y donde existe el límite de las cuerdas.
x general da una función derivada, que se puede usar para calcular la pendiente de la función original en varios puntos.
Notación Derivada
Para la derivada con respecto a x , lo que significa que la variable dependiente para una función f ( x ) es x , es f ʹ ( x ) o df ( x )/ dx . El dx indica un cambio incremental en la variable x , y df ( x ) indica un cambio incremental en f ( x ). Los cambios incrementales se llaman diferenciales.
Fórmulas Derivadas
La derivada se puede encontrar por el límite anterior, pero normalmente es a través de una fórmula que se trabaja para encontrar una derivada. Quizás la más básica de estas fórmulas es que la derivada de f ( x ) = x n está dada por d ( x n )/ dx = nx n -1 .
Esto se verificará a continuación para n = 2 y para n = ½.
Primero, para n = 2 tenemos los siguientes pasos.
Ejemplo de forma límite de derivada
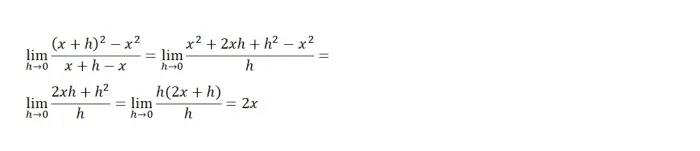
A continuación, para n = ½ tenemos los siguientes pasos.
segundo ejemplo
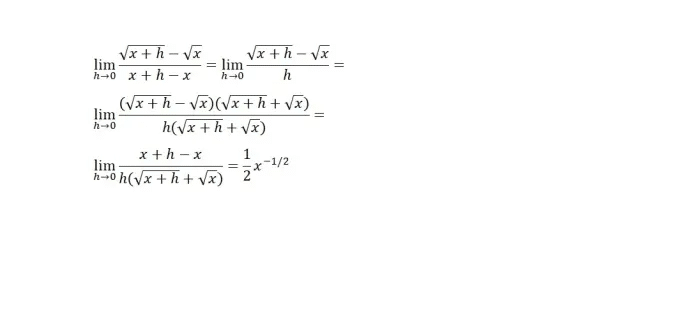
Observe que lo anterior requería racionalizar el numerador. Esto es lo contrario de lo que normalmente se hace en álgebra. La principal dificultad en todo el cálculo es pensar fuera de la caja del álgebra. Las técnicas de cálculo no son tan difíciles.
Una fórmula diferente es la fórmula para la derivada de sin( x ), que es cos( x ). Esto se muestra fácilmente usando la fórmula del seno de la suma de dos ángulos.
El tercer ejemplo
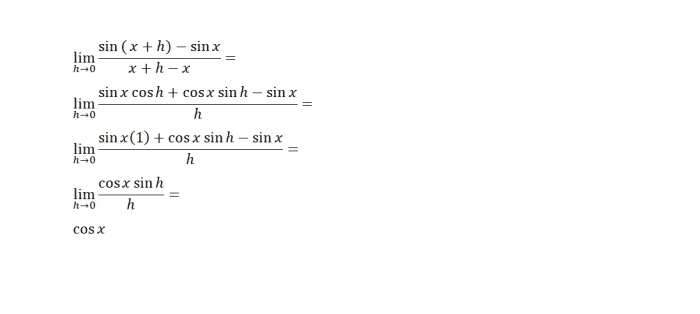
Encontrar una derivada en un valor dado
Encuentra la pendiente de la línea f ( x ) = x 3 en x = 4.
Encuentre df (4)/ dx .
d ( x 3 ) / dx = 3×2
3(4) 2 = 48
Combinar funciones
A las combinaciones de funciones se les puede tomar su derivada. Al trabajar con funciones complejas, es una buena idea manejar la función como partes más pequeñas cuyas derivadas son de forma conocida.
La derivada de un múltiplo constante de una función es la constante multiplicada por la derivada de la función. Dado que la constante podría factorizarse y luego sacarse del límite, esto es fácil de explicar.
d ( cf ( x )/ dx = cdf ( x )/ dx
La derivada de la suma de dos funciones es la suma de las derivadas de las funciones.
re ( f + gramo )( x )/ dx = df ( x )/ dx + dg ( x )/ dx
La derivada de la diferencia de dos funciones es la diferencia de las derivadas de las funciones.
re ( f – g )( x )/ dx = df ( x )/ dx – dg ( x )/ dx
La derivada del producto de dos funciones viene dada por la siguiente fórmula.
re ( fg ( x ))/ dx = f ( x )( dg ( x )/ dx ) + g ( x )( df ( x )/ dx )
La función cociente ( f / g )( x )/ dx , g ( x ) ≠ 0, tiene la derivada dada por la siguiente fórmula.
re ( f / g )( x )/ dx = [ g ( x ) df ( x )/ dx – f ( x ) dg ( x )/ dx ]/( g ( x ) 2 )
La derivada de la función compuesta, f ( g ( x ) viene dada por la siguiente fórmula.
df ( gramo ( x )/ dx = df ( gramo ( x ) / dg ( x ) · dg ( x ) / dx
Diferenciación implícita y diferenciación logarítmica
La diferenciación implícita es necesaria cuando la variable dependiente es difícil de aislar. En tal caso, la función y de x, y ( x ), se deriva como una función compuesta.
A continuación se muestra un ejemplo de diferenciación implícita.
Encuentre dy / dx cuando ln( y ) = x 2 .
La derivada de ln( x ) es 1/ x . Entonces la derivada de ln y es (1/ y ) dy / dx.Observe que y es una función de x , por lo que usamos la diferenciación implícita.
(1/ y ) dy / dx = 2 x resulta de tomar la derivada de cada lado de la ecuación original.
Resolviendo para dy / dx se obtiene la derivada deseada.
dy / dx = 2 xy
Esta técnica es necesaria para encontrar la derivada donde la variable independiente se presenta en un exponente.
Encuentra la derivada de y ( x ) = 3 x
Toma el logaritmo de cada lado de la ecuación.
ln( y ) = ln(3 x )
ln( y ) = x ln(3)
(1/ y ) dy / dx = ln3
dy / dx = y ln3
Sustituye a y .
dy / dx = 3 x ln3
Derivados Superiores
Es posible tomar derivados de derivados. Los símbolos para la segunda y tercera derivada son, respectivamente, d 2 f (x )/ dx 2 y d 3 f (x )/ dx 3 .



